Often people will say they don’t understand my blogs, so this one is split into three bits (imitating nature as we shall see) depending on how much physics you care to know.
Bit one: the standard model
The standard model is a theory about our best knowledge of particle physics to date, and it includes a toolkit of particles with which you can build a universe from. Each of these particles has different properties, but there are lots of patterns and links between them (just like the periodic table in chemistry).
There are two types of particles overall- the ones that make up stuff– the matter particles, and the ones that make the stuff do stuff– the ones that carry the forces. I am only talking about the matter ones in this blog 🙂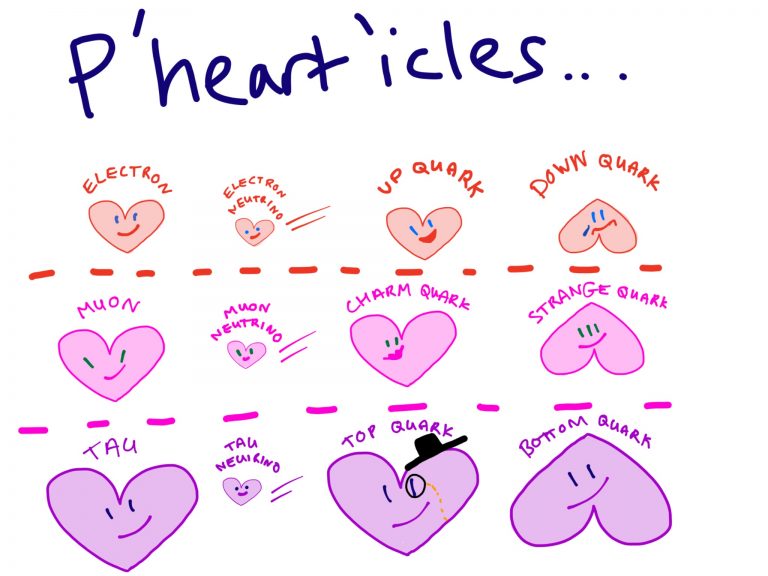
All the matter particles are laid out in this snazzy diagram I have drawn– they are hilariously titled p’heart’icles what with Valentine’s Day coming up 😛
Bit two: why the three rows?
The top row of phearticles includes a electron, an up quark and a down quark, which are the things you need to make up all everyday matter like you and me and planets. Until the muon was spotted, everyone thought they were all that the universe was made up of. A particle physicist at the time of the muon’s discovery, I.I. Rabi, was famously meant to have asked of its existence: ‘who ordered that?’
The muon is on row two– it is the same as the electron but is just heavier. Everyone was baffled about why the universe had come up with this heavier version of the electron– especially as it didn’t seem to be using it.
After this discovery, all the other particles were eventually filled in on rows two and three. Each one on row two is a heavier version of the particles above it, and row three particles are the same again, but heavier still. Queerer and queerer.
When I first heard about this feature of the standard model, I thought ‘oh yeah well obviously there are going to be loads more generations of still heavier particles, but our particle accelerators can’t access energies high enough to create them yet’.
(Coz E= mc^2 and all that so you need higher energies to get more massive particles.)
This seems reasonable. Who is to say there isn’t another fourth, even heavier electron type thing lurking out there?
Bit three: I am to say there are only three generations 🙂
The proof for this comes from a simple experiment, but before that we have to consider the little neutrino phearticles. These are not like the other particles of the three generations, because there is not a big increase in mass between the rows. Until recently neutrinos were thought to have no mass at all, but it was then discovered that they change type as they are flying along– a phenomenon that means they must have a small mass difference i.e. they can’t all have zero mass!
Because the masses are so tiny, and neutrinos hardly react with anything at all, their masses haven’t been measured exactly, and it isn’t even known if they follow the same pattern as the other generations– getting heavier as they go down the rows.
However, because they have such small masses, it would be fair to assume that another fourth of fifth generation of matter particles would also contain a very light neutrino. This means we should be procuring neutrinos of any extra generations in particles accelerators all the time– E= mc^2 again.
An example of a reaction that should produce them is when two electrons collide and produce a Z boson (which is a type of force particle that I said we would be ignoring). This Z phearticle can decay into any of the other matter particles, including the three neutrinos. If there was a fourth generation, it would be reasonably expected to decay to this generation’s neutrino as well. However you can measure a lot of these reactions and measure the amount of times it decays to each of the different particles. As neutrinos don’t really react with anything, they are usually ‘seen’ by looking at the amount of missing energy. The amount of missing energy that is seen in millions and millions of these decays is exactly equal to the amount of energy needed to produce three generations of neutrinos. Hence, we have only three generations of particles.
I still find that weird… Why three generations? It turns out with less than three some crucial aspects of the strong force wouldn’t work out, but why not ten generations or fifteen? 😛
I can’t answer that just yet, so instead I leave you with some more cute phearticles…
Leave a Reply
This site uses Akismet to reduce spam. Learn how your comment data is processed.
